백준 2775 부녀회장이 될거야(Java)

아. 또 핵인싸 한 분이 사람을 피곤하게 하는 문제를 만든 듯 하다..

문제

평소 반상회에 참석하는 것을 좋아하는 주희는 이번 기회에 부녀회장이 되고 싶어

각 층의 사람들을 불러 모아 반상회를 주최하려고 한다.

이 아파트에 거주를 하려면 조건이 있는데,

“a층의 b호에 살려면 자신의 아래(a-1)층의 1호부터 b호까지 사람들의 수의 합만큼 사람들을 데려와 살아야 한다”

는 계약 조항을 꼭 지키고 들어와야 한다.

아파트에 비어있는 집은 없고 모든 거주민들이 이 계약 조건을 지키고 왔다고 가정했을 때,

주어지는 양의 정수 k와 n에 대해 k층에 n호에는 몇 명이 살고 있는지 출력하라.

단, 아파트에는 0층부터 있고 각층에는 1호부터 있으며, 0층의 i호에는 i명이 산다.

입력

첫 번째 줄에 Test case의 수 T가 주어진다.

그리고 각각의 케이스마다 입력으로 첫 번째 줄에 정수 k, 두 번째 줄에 정수 n이 주어진다

출력

각각의 Test case에 대해서 해당 집에 거주민 수를 출력하라.

제한

1 ≤ k, n ≤ 14

출처 https://www.acmicpc.net/problem/2775

2775번: 부녀회장이 될테야

---

먼저 문제의 조건

“a층의 b호에 살려면 자신의 아래(a-1)층의 1호부터 b호까지 사람들의 수의 합만큼 사람들을 데려와 살아야 한다”

을 엑셀에 그려보자.

맨 첫 층이 0층이고, 0층의 1~14호는 호수만큼의 사람들이 살게 된다.

그리고 각 층 1호는 1명이고, 14층까지 있다.

사실 여기서 처음 풀 때는 종이에 풀면서 1~n까지의 합 시그마로 나타내는 걸 생각했는데,

이게 층이 올라가면 갈수록 수식화가 복잡해진다.

시그마 두 개 이상이 겹쳐지면 수능 본 지 한참인 굳은 머리는 어 이게 아닌데 라고 생각하고 작동을 멈춰버려서

마저 엑셀에 그려보았다.

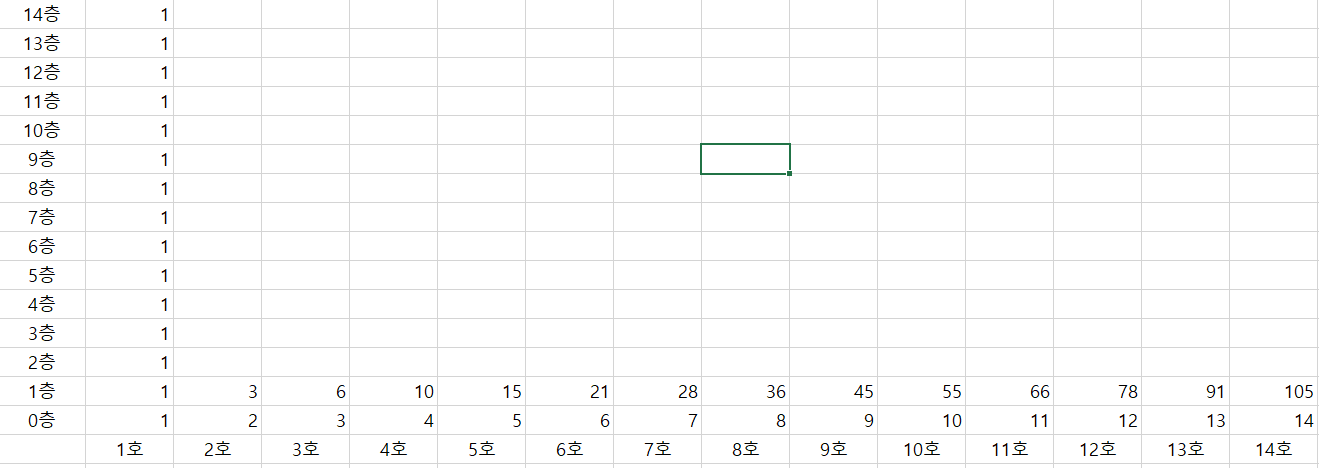
1층 2호에 살려면 자신의 아래 0층의 1호부터 2호까지 사람들의 수의 합만큼 사람을 데려와야 한다.

1+2 = 3이다.

1층 3호에 살려면 자신의 아래 0층의 1호부터 3호까지 사람들의 수의 합만큼 사람을 데려와야 한다.

1+2+3 = 6...인데 가만있어봐.

1층 2호의 3 + 0층 3호의 3 = 6이네?

계속 그려보았다.

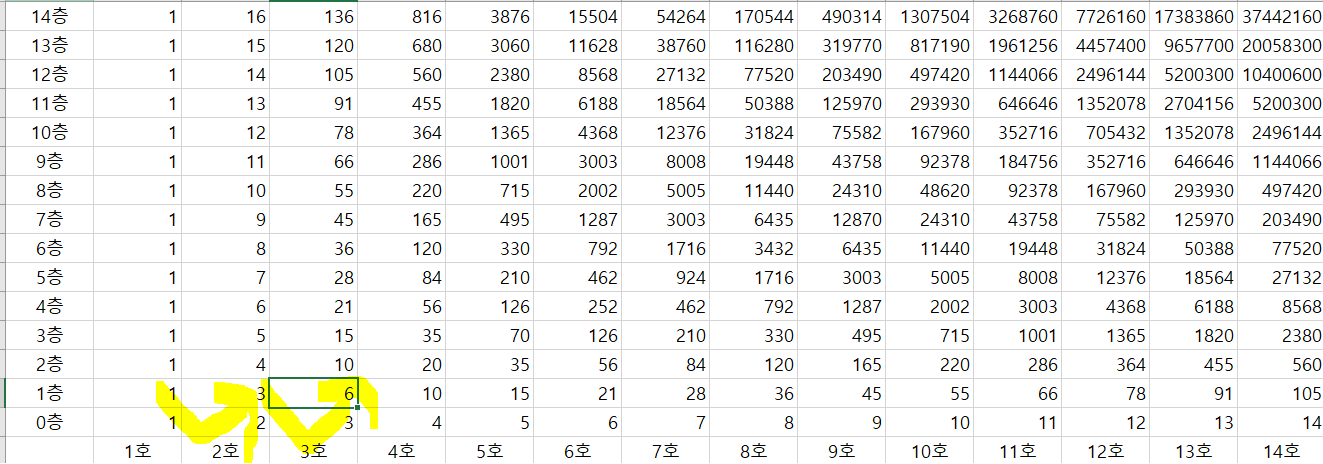
0층, 1호를 제외하고는 a-1층b호 + a층 b-1호 점화식 꼴로 그려짐을 확인할 수 있었다.

그리고 이를 다음과 같은 코드로 나타냈다.

import java.io.*;

public class Main{
    public static int [][] apt = new int [15][15];
    
    public static void main(String[] args) throws IOException{
       
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int T = Integer.parseInt(br.readLine());    //테스트케이스 갯수
        
        makeApt();        
        
        for (int i = 0 ; i < T ; i++){
            int k = Integer.parseInt(br.readLine());    //k층
            int n = Integer.parseInt(br.readLine());    //n호
            
            System.out.println(apt[k][n]);    //k층 n호의 거주자수 : makeApt()에서 구해온값 소환
        }
        
        
    }
    //아파트 생성
    public static void makeApt(){
        for (int i = 0 ; i < 15 ; i++){
            apt[i][1] = 1;    //각층 1호는 1명
            apt[0][i] = i;    //0층 i호는 i명
        }
        
        for (int i = 1; i < 15; i++){    //1~14층
            for (int j = 2; j < 15; j++){    //2~14호 : 아까 0층이랑, 1호라인 먼저셋팅함
                apt[i][j] = apt[i-1][j] + apt[i][j-1];    //a-1층 b호 + a층 b-1호의 합
            }
        }
    }
}

2차원 배열을 만들고 makeApt() 함수를 통해 값을 미리 도출해놓는다.

0층, 1호는 미리 셋팅할 수 있고, 1~14층의 2~14호는 2중 for문을 통해 점화식을 계산하도록 설계한다.

그리고 나서 k층 n호 값을 입력하면 해당 번지 값을 바로 호출할 수 있다.